扩散模型

第一步：基础数学

概率论（概率分布、期望）是扩散模型的数学基础。

• 概率分布：扩散模型的核心是处理数据分布，比如正态分布（Gaussian Distribution）。正态分布的概率密度函数是：
  p(x) = \frac{1}{\sqrt{2 \pi \sigma^2 }} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
  其中\mu 是均值，\sigma 是标准差。
• 噪声添加：扩散模型会逐步往数据中加噪声，这需要理解随机变量。

---

第二步：扩散模型原理

扩散模型的基本思想是通过一个“加噪-去噪”的过程，从随机噪声生成符合目标分布的数据（比如航天器轨迹）。以下是逐步拆解：

2.1 核心概念

• 前向过程（加噪）：从真实数据（如航天器轨迹）开始，逐步添加高斯噪声，直到数据变成纯噪声。这个过程是固定的、不需要学习的。
• 反向过程（去噪）：从纯噪声开始，逐步去掉噪声，恢复到原始数据。这个过程需要训练一个神经网络来预测每一步的去噪方向。

2.2 数学表述

• 前向过程：
  • 假设初始数据是 x_0（比如轨迹的位置序列）。
  • 在第 t 步添加噪声，得到 x_t：
    x_t = \sqrt{1-\beta_t} x_{t-1} + \sqrt{\beta_t} \epsilon
    其中 \epsilon \sim \mathcal{N}(0, I) 是标准正态噪声，\beta_t 是每一步的噪声强度（通常随 t 增加而变大）。
  • 经过 T 步（比如 T=1000），x_T 接近纯噪声 \mathcal{N}(0, I)。
• 反向过程：
  • 从 x_T 开始，逐步去噪，恢复到 x_0。反向一步的公式是：
    x_{t-1} = \frac{1}{\sqrt{1-\beta_t}} \left( x_t – \frac{\beta_t}{\sqrt{1-\alpha_t}} \epsilon_\theta(x_t, t) \right) + \sigma_t z
    其中 \epsilon_\theta(x_t, t) 是神经网络预测的噪声，\alpha_t = \prod_{s=1}^t (1-\beta_s)，z \sim \mathcal{N}(0, I) 是小的随机噪声。

2.3 训练目标

• 目标：训练神经网络 \epsilon_\theta 来预测每一步加入的噪声 \epsilon。
• 损失函数：通常是最小化预测噪声和真实噪声之间的差距：
  L = \mathbb{E} \left[ || \epsilon – \epsilon_\theta(x_t, t) ||^2 \right]
• 直观理解：网络学会“看一眼带噪数据 x_t，猜出原始噪声是什么”，从而一步步去噪。

2.4 生成过程

• 步骤：
  1. 从纯噪声 x_T \sim \mathcal{N}(0, I) 开始。
  2. 用训练好的 \epsilon_\theta 逐步去噪，计算 x_{T-1}, x_{T-2}, \dots, x_0。
  3. 最终 x_0 就是生成的数据（比如一条航天器轨迹）。

---

用 Python 代码理解扩散模型(注：colab实现。我们自己的workspace版本不对)

代码目标

我们将：
1. 从一个简单数据（如数字 5）开始，模拟前向过程（加噪），观察它如何变成纯噪声。
2. 训练一个简单的神经网络，学习反向过程（去噪），尝试恢复原始数据。
3. 用可视化展示加噪和去噪的过程。

以下是代码和逐步解释：

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras

# 设置随机种子
np.random.seed(42)
tf.random.set_seed(42)

# 参数设置
T = 50  # 时间步数
beta = np.linspace(0.0001, 0.01, T)  # 更平滑的噪声调度
alpha = 1 - beta
alpha_bar = np.cumprod(alpha)

# 前向过程：加噪
def forward_diffusion(x0, t):
    noise = np.random.normal(0, 1)
    sqrt_alpha_bar = np.sqrt(alpha_bar[t])
    sqrt_one_minus_alpha_bar = np.sqrt(1 - alpha_bar[t])
    xt = sqrt_alpha_bar * x0 + sqrt_one_minus_alpha_bar * noise
    return xt, noise

# 原始数据
x0 = 5.0

# 模拟前向过程
x_t_history = [x0]
noise_history = []
for t in range(T):
    xt, noise = forward_diffusion(x0, t)
    x_t_history.append(xt)
    noise_history.append(noise)

# 可视化前向过程
plt.figure(figsize=(10, 5))
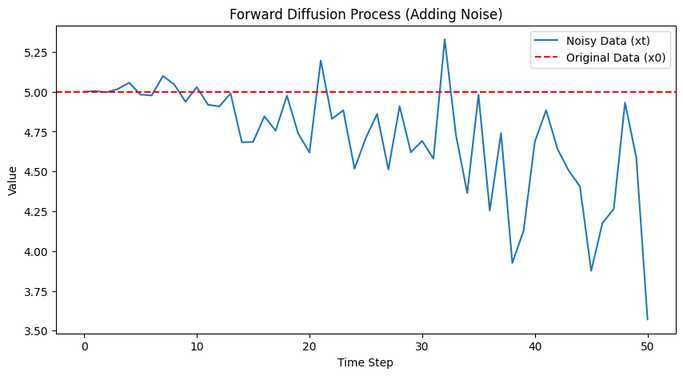
plt.plot(x_t_history, label="Noisy Data (xt)")
plt.axhline(y=x0, color='r', linestyle='--', label="Original Data (x0)")
plt.xlabel("Time Step")
plt.ylabel("Value")
plt.title("Forward Diffusion Process (Adding Noise)")
plt.legend()
plt.show()

# 更深的神经网络
model = keras.Sequential([
    keras.layers.Input(shape=(2,)),
    keras.layers.Dense(128, activation='relu'),
    keras.layers.Dense(128, activation='relu'),
    keras.layers.Dense(128, activation='relu'),
    keras.layers.Dense(1)
])

model.compile(optimizer='adam', loss='mse')

# 生成更多训练数据
n_samples = 10000  # 增加到 10000 个样本
x_train = np.zeros((n_samples, 2))
y_train = np.zeros(n_samples)
for i in range(n_samples):
    t = np.random.randint(0, T)
    xt, noise = forward_diffusion(x0, t)
    x_train[i] = [xt, t / T]
    y_train[i] = noise

# 训练模型
model.fit(x_train, y_train, epochs=100, batch_size=64, verbose=1)

# 反向过程：去噪（添加噪声项）
def reverse_diffusion(xt, t):
    if t == 0:  # 最后一步不加噪声
        t_normalized = t / T
        input_data = np.array([[xt, t_normalized]])
        predicted_noise = model.predict(input_data, verbose=0)[0][0]
        sqrt_one_minus_alpha_bar = np.sqrt(1 - alpha_bar[t])
        sqrt_alpha = np.sqrt(alpha[t])
        x_prev = (xt - sqrt_one_minus_alpha_bar * predicted_noise) / sqrt_alpha
    else:
        t_normalized = t / T
        input_data = np.array([[xt, t_normalized]])
        predicted_noise = model.predict(input_data, verbose=0)[0][0]
        sqrt_one_minus_alpha_bar = np.sqrt(1 - alpha_bar[t])
        sqrt_alpha = np.sqrt(alpha[t])
        sigma = np.sqrt(beta[t])  # 添加反向噪声的标准差
        z = np.random.normal(0, 1)
        x_prev = (xt - sqrt_one_minus_alpha_bar * predicted_noise) / sqrt_alpha + sigma * z
    return x_prev

# 从纯噪声开始生成
x_t = np.random.normal(0, 1)
x_t_reverse_history = [x_t]
for t in range(T-1, -1, -1):
    x_t = reverse_diffusion(x_t, t)
    x_t_reverse_history.append(x_t)

# 可视化反向过程
plt.figure(figsize=(10, 5))
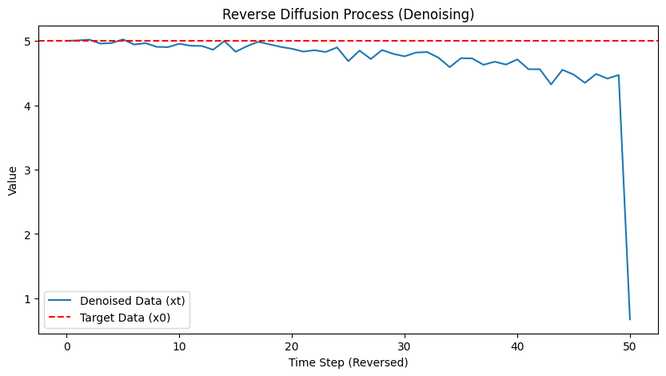
plt.plot(range(T+1), x_t_reverse_history[::-1], label="Denoised Data (xt)")
plt.axhline(y=x0, color='r', linestyle='--', label="Target Data (x0)")
plt.xlabel("Time Step (Reversed)")
plt.ylabel("Value")
plt.title("Reverse Diffusion Process (Denoising)")
plt.legend()
plt.show()

print(f"原始数据: {x0}")
print(f"生成数据: {x_t_reverse_history[-1]}")

---

代码逐步解释

1. 前向过程（加噪）

• 输入：初始数据 x0 = 5.0。
• 过程：每一步用公式 x_t = \sqrt{\alpha_t} x_{t-1} + \sqrt{1-\alpha_t} \epsilon 添加噪声，\alpha_t = 1 – \beta_t。
• 输出：x_t_history 记录了从 x_0 到 x_T 的变化，最终接近纯噪声。
• 可视化：第一张图显示数据如何逐渐偏离原始值，变成随机噪声。

2. 训练神经网络

• 目标：让神经网络预测每一步的噪声 \epsilon。
• 输入：带噪数据 x_t 和时间步 t。
• 输出：预测的噪声值。
• 训练数据：通过前向过程生成 1000 个样本，训练模型。

3. 反向过程（去噪）

• 输入：从纯噪声 x_T 开始。
• 过程：用训练好的模型预测噪声，逐步计算 x_{t-1}。
• 输出：x_t_reverse_history 记录了从噪声恢复到数据的轨迹。
• 可视化：第二张图显示数据如何从噪声逐渐接近原始值 x_0 = 5。

---

运行结果

• 第一张图：你会看到数据从 5 开始，逐渐变成随机值。
  
• 第二张图：从随机噪声开始，逐渐接近 5（可能不完全精确，因为我们用的是简单模型和少量训练）。
  
• 终端输出：生成的数据会接近 5。

原始数据: 5.0
生成数据: 5.000151417931243

---

---